Programming Fundamentals - part 1 of 2
Foreword
We begin our investigation of programming fundamentals by reviewing the number systems most commonly used in computer science and programming languages. We consider the binary, decimal, hexadecimal, and octal number systems. It is important to understand that the methods used below to describe one number systems can be used to explain other number systems. So even though we do not consider an unusual number system such as base 12, it should be easy enough to describe that system using the same techniques shown below.
Generic Number System
Before reviewing number systems most commonly used in computing, the applied number systems, let's consider the generic foundation of all number systems. We begin with the concept of radix, which is the base and also the name of each number system. For example, base 10 is decimal, base 2 is binary, base 16 is hexadecimal, and base 8 is octal.
In the generic table below, the first row includes the base raised to incrementally higher exponents. The next row is the result of the exponentiation, called the power. The third row includes symbols from the specific number system. For instance, decimal uses the numbers 0-9 so the symbol row could contain any symbol from 0-9. Since binary uses the symbols 0 and 1, the symbol row for the binary system would contain 0's and 1's. The next row is the result of multiply the power cells with the symbol cells so it is named the product row. In the last row of the table, all products are added to produce the sum which is the value in decimal.
The rows in the generic table are:
- base raised
- powers
- symbols
- products
- sum
Using the methods of the generic number system, we could demonstrate a variety of 'wild' systems like base 19, base 33, or even base 777. What would be the challenge of a base 777 number system? That's right, selecting 777 symbols to represent each number in the system.
| Generic Number System | ||||||||
| base7 | b6 | b5 | b4 | b3 | b2 | b1 | b0 | |
| power7 | pow6 | pow5 | pow4 | pow3 | pow2 | pow1 | pow0 | |
| x | symbol7 | s6 | s5 | s4 | s3 | s2 | s1 | s0 |
| = | product7 | p6 | p5 | p4 | p3 | p2 | p1 | p0 |
| p7 + p6 + p5 + p4 + p3 + p2 + p1 + p0 = sum | ||||||||
Applied Number Systems
It seems appropriate to initiate our discussion of programming fundamentals by reviewing applied number systems. We are most familiar with the decimal system which is the prevalent system in use worldwide. The decimal system uses radix 10 (base 10). Even though we think in decimal terms, we might not understand how the system is derived. We can derive the decimal number using the same operations we used in the binary, hexadecimal, and octal tables shown below. Naturally, understanding the value of a decimal number is second nature so we really don't have to perform the operations of multiplication and addition by each exponential place. However, it is important to understand that decimal numbers are constructed using the same methods of the other number systems.
| Decimal | ||||||||
| 107 | 106 | 105 | 104 | 103 | 102 | 101 | 100 | |
| 10000000 | 1000000 | 100000 | 10000 | 1000 | 100 | 10 | 1 | |
| x | 0 | 3 | 5 | 9 | 2 | 6 | 8 | 7 |
| = | 0 | 3000000 | 500000 | 90000 | 2000 | 600 | 80 | 7 |
| 0 + 3000000 + 500000 + 90000 + 2000 + 600 + 80 + 7 = 3,592,687 | ||||||||
The binary system is the most elemental number system used in computing. In binary, one digit is called a bit, four bits a nibble (or nybble), and eight bits a byte. The definition of the term word when referring to number of bits varies. It usually means the number of bits in the CPU registers so it is commonly 16, 32, or 64-bits. In the formative days of computing, binary was originally used to identify the presence (1) or absence (0) of an electrical charge. There are two digits used in the binary system and those two numbers can be combined to represent any positive numerical value. Binary, meaning two, consists of the numbers 1 and 0. In the first row below, the number 2 is called the radix (a.k.a. base 2). It is raised to the powers 0 - 7. The first row of all number systems consist of the radix raised to values starting at 0. Recall from basic math class that any number raised to 0 is equal to 1.
The second row contains values of the resulting exponential operation. For instance, 27 = 128, 24 = 16, etc. How do we convert a binary number to its decimal equivalent? The binary number 10101101 is provided as an example. To determine the decimal equivalent of that binary number, perform the appropriate multiplications and additions shown in the table. Note the value of 1 set on the third row in the 25 position. This means that 32 should be multiplied by that 1 to produce 32 which is then added with the results from the other positions. The appropriate operations show that 10101101 in binary = 173 in decimal.
| Binary | ||||||||
| 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 | |
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |
| x | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| = | 128 | 0 | 32 | 0 | 8 | 4 | 0 | 1 |
| 128 + 0 + 32 + 0 + 8 + 4 + 0 + 1 = 173 | ||||||||
Since binary numbers are difficult to read, another popular number system was developed. In computing, the hexadecimal (hex) system is ubiquitous. The hex system has the number 16 as its radix (base 16). Only one hex digit is required to represent every four binary digits. Hex numbers are seen throughout computing in values such as colors, address locations, and assembly language instructions.
Hex numbers are identified by a leading '0x' as in '0x7E23FA'. Sometimes they are shown with a lowercase 'h' such as '7Dh'. Observe the letters in the third row of the hexadecimal table. Why are the letters E, F, and A used? In the binary system we needed two digits (0 and 1) and in the decimal system we needed ten digits (0-9) to represent the numbers. In the hex system we need 16 digits. However, we only have ten digits, 0-9 symbols with which to work. Therefore, we need six more symbols. Since we are out of numerical symbols after 0 - 9, we use first six letters from the alphabet A -F. So, A = 10, B = 11, C = 12, D = 13, E = 14, F = 15. Using the symbols 0-9 and A-F, we now have 16 symbols with which to work.
Now consider the hex number '0x7E23FA' as shown in the table. How do we obtain the decimal equivalent of that number? We use the same technique as that used for binary and decimal numbers. For instance, 164 = 65536. Recall that E = 14. So, if we have E in the 164 position, we multiply 65536 x 14 = 917540 as shown. Perform the same multiplication operation for the other positions in the table, add the products to obtain the decimal equivalent of '0x7E23FA' which we see to be 8,266,746.
| Hexadecimal | ||||||||
| 167 | 166 | 165 | 164 | 163 | 162 | 161 | 160 | |
| 268435456 | 16777216 | 1048576 | 65536 | 4096 | 256 | 16 | 1 | |
| x | 0 | 0 | 7 | E | 2 | 3 | F | A |
| = | 0 | 0 | 7340032 | 917504 | 8192 | 768 | 240 | 10 |
| 0 + 0 + 7340032 + 917504 + 8192 + 768 + 240 + 10 = 8,266,746 | ||||||||
There are only eight numbers required/used in the octal system. Seeing numbers expressed in octal is less common than it was in the early days of computing. Early computers had 12, 24, or 32-bit address spaces and each of those is divisible by three. One octal number can be used to represent three binary digits so it was a convenient method for referencing addresses.
However, more recently, computers are using 32 and 64-bit addressing so the hex system is more compatible since both 32 and 64 are divisible by 16 and can be more succinctly described than with octal digits. For instance, the 16-bit binary number 11001110 11110001 is equal to CEF1 in hex and 147361 in octal. Two more digits are required to represent the number in octal compared to hex. Octal can still be found in computing applications such as setting Unix file permissions.
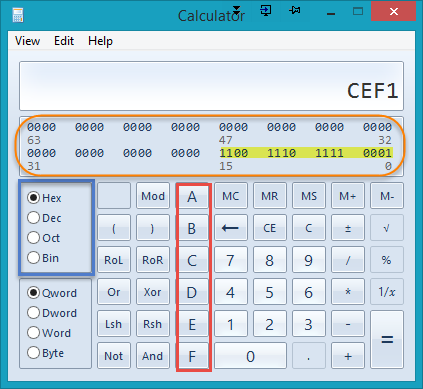
The calculator that ships with Windows 10 includes a programmer version which can be accessed via the View menu. In the image below, I originally entered the binary number (highlighted) and then selected 'Hex' to see the hex equivalent. Note that the binary number is still displayed. And, the binary values can be edited from positions 0 - 63 in the orange oval section. The radix can be selected in the blue rectangle section. Note the letters A - F that are enabled when Hex is selected.
In the past, there have been a variety of ways to identify octal numbers. A consensus is building for the octal naming to emulate the hexadecimal model and use a '0' followed by a lowercase o much like the '0x' that is used with hex numbers. The result appears like: '0o4721', '0o1381', and '0o9835'. The '0o' is the standard now being followed by ECMAScript 6 (JavaScript), Haskell, Perl, Python, and Ruby.
The same multiplication and addition operations that were used in the binary and hex systems above are applicable to octal. So, in the example below, the octal number 0o20053107 is equal to the decimal number 4,216,391.
| Octal | ||||||||
| 87 | 86 | 85 | 84 | 83 | 82 | 81 | 80 | |
| 2097152 | 262144 | 32768 | 4096 | 512 | 64 | 8 | 1 | |
| x | 2 | 0 | 0 | 5 | 3 | 1 | 0 | 7 |
| = | 4194304 | 0 | 0 | 20480 | 1536 | 64 | 0 | 7 |
| 4194304 + 0 + 0 + 20480 + 1536 + 64 + 0 + 7 = 4,216,391 | ||||||||
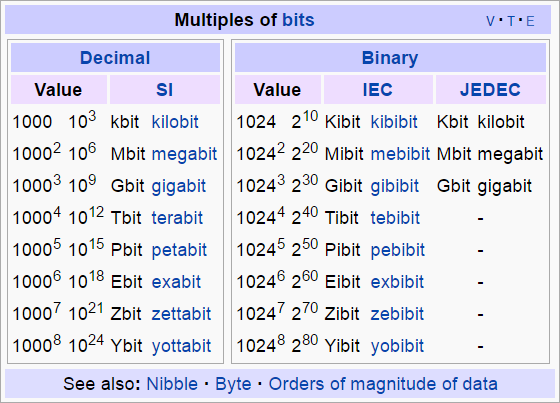
Multiples of bits by orders of magnitude (powers of 10) are assigned names per the chart below.
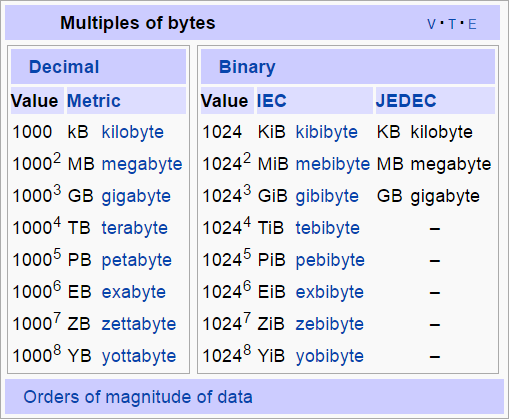
Multiples of bytes by orders of magnitude (powers of 10) are assigned names per the chart below.
Both charts above are courtesy of Wikipedia. By the way, is Wikipedia accurate? See this article.

