Data Types
Foreword
In this course, we cover the most commonly used Python data types as outlined in the Python Language Reference.
The following four general data types are discussed in the course and, unless otherwise stated, will be used in examples:
- Numbers (Integer, Boolean, Real, Complex)
- Sequences (Immutable - String, Tuple, Bytes; Mutable - Lists, Byte Arrays)
- Mappings (Dictionary)
- Sets
Tuples are created with parentheses () (and no parentheses; the default), lists are created with square brackets [], dictionaries and sets are both created with braces {}. Sets are covered below.

Data Types - Sets
Sets - an unordered collection of unique and immutable objects. Even though sets cannot contain mutable objects such as lists, sets themselves are mutable.
- Use constructor set() to create a new set
- Use {<insert contents here>} to create a new set
- Use braces with ellipses '{...}' to create empty set
- Sets are mutable (except frozen sets)
- Objects in sets are unordered (i.e. do not have an index)
- Objects can be of different types
- Objects in set must be unique
- Objects in set must be immutable (no lists in sets)
- Frozen Set - special type of set that is not mutable

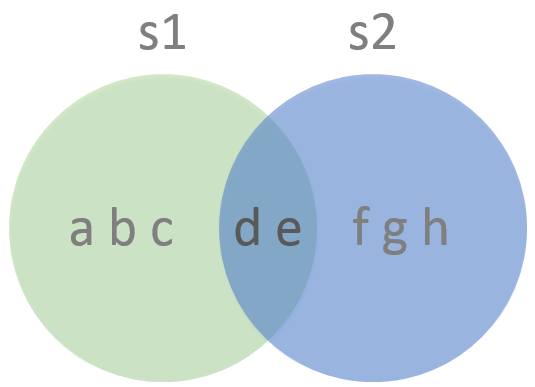
The set data type is useful for emulating the mathematical operations of set theory. For instance, using the set operations, we can evaluate the mathematical set theory functions of union, intersection, difference, and symmetric difference. See the Venn diagram below. The set operations yield the following:
- Union of S1 and S2 = abcdefgh
- Intersection of S1 and S2 = de
- Difference of S1 - S2 = abc
- Difference of S2 - S1 = fgh
- Symmetric Difference of S1 and S2 = abcfgh
The table below contains many of the operations that can be performed on sets. Note: some operations do not apply to frozen sets which are immutable.
| Set Operations | |
| set() | constructor for set type |
| x in s | True if x in s |
| x not in s | True if x not in s |
| len(s1) | returns # of elements in the set |
| s1.add(e) | add element to set |
| s1.copy() | return a shallow copy |
| s1.update(s2) | adds s2 to s1 |
| s1.remove(e) | removes element e; error if not found |
| s1.discard(e) | removes element e; NO error if not found |
| s1.clear() | removes all elements |
| s1.union(s2) | returns all elements from both; same as s1 | s2 |
| s1.intersection(s2) | returns elements in common |
| s1.difference(s2) | in s1 but not in s2; same as s1 - s2 |
| symmetric_difference() | returns elements not shared |
| s1.issubset(s2) | True if s1 a subset of s2 |
| s1.issuperset(s2) | True if s1 a superset of s2 |
| s1.isdisjoint(s2) | True if sets have NO common elements |
| s1.pop() | return and remove an arbitrary element |
| frozenset() | constructor for frozenset type |
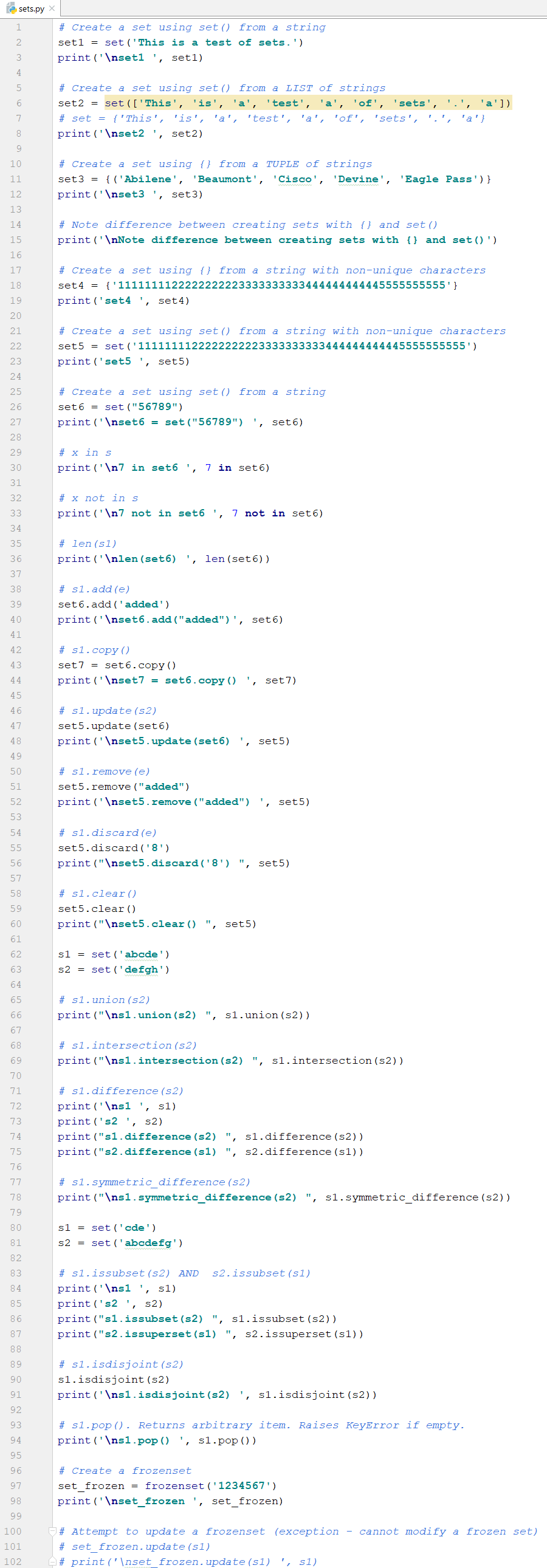
The code below demonstrates each of the set operations in the table above. s.copy() is covered more thoroughly in the chapter Copy Operations. Note the highlight added by PyCharm on line 6. This is an advisory that the function call set() on line 6 which uses the set() constructor can be replaced with a set literal. The set literal alternative is shown on line 7. Note the difference between creating sets with set literals and set constructors on lines 18 and 22.
Here's the output.